This is going to scaling sets of numbers so if you are bored already now is a good time to go and browse something else. A friend at work asked how do I round a set of values to the nearest value with an increment of 0.5. Why would you want that you might ask? Its useful for scaling data by specific increments like for driving values along a curve.u value to create stepped noise without using a ramp. Here is how you do it.
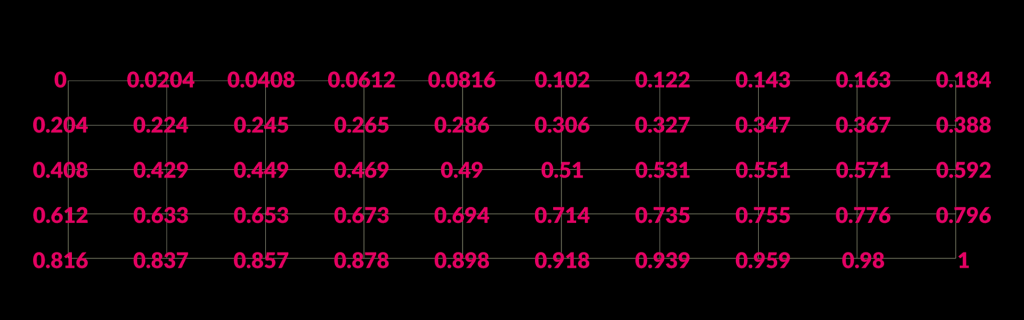
The grid above has an attribute going 0 to 1 linearly and I want to change it so it steps in increments of 0.2 so the result is 0.2, 0.4, 0.8, 1.0. The trick to do that is to divide by the step size 0.2 in this case the round the value and them multiply by the step size again to scale the value back to the original range. For example lets take the middle value of 0.51 and divide by 0.2 and that returns 2.55, now apply the ceil() function and that returns 3. Lastly multiple by 0.2 and that returns 0.6. Applying that to the grid looks like this:
float seed = float(@ptnum) / (@numpt-1); //initial values
seed /= 0.2;
seed = ceil(seed);
seed *= 0.2;
s@test = sprintf("%.3g",seed);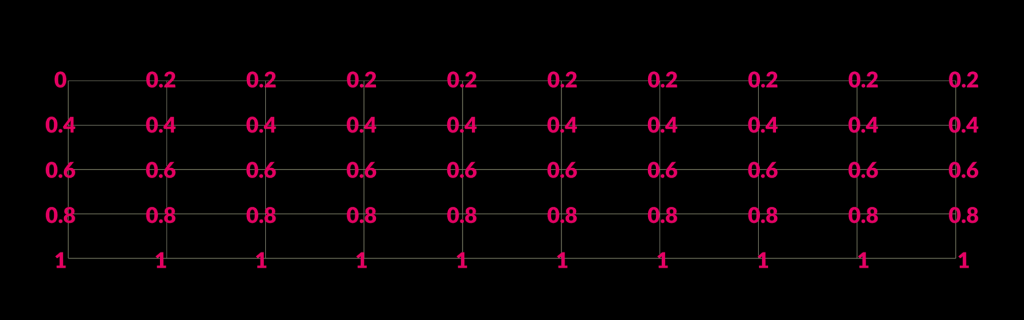
So that is cool but there is a slightly longer way to get the same result and that is by multiplying by 100 and the dividing by 2 before rounding and then doing the reverse after. It’s a bit more convoluted but it allows you to control what decimal place to round to separately from step size.
float seed = float(@ptnum) / (@numpt-1); //initial values
seed *= 10;
seed /= 2;
seed = ceil(seed);
seed *= 2;
seed /= 10;
s@test = sprintf("%.3g",seed);With that in mind here are two examples one with a 0.04 increment and one and increment of 25 with with a random value range of between 0 and 100.
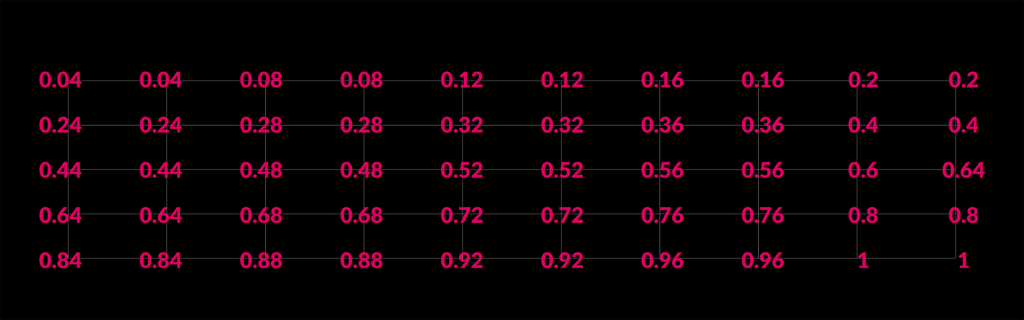

That is for messing around with numbers for now. Here is the hip file.
